Основные понятия и определения
3 можно выполнять только после того, как и молоко и вода вскипят; очевидно, также, что работа a
4 не может быть начата до тех пор, пока все работы a
1, a
2 и a
3 не будут окончены.
Замечания:
1. В общем случае разбиение большой программы (плана) на множество работ не единственно. Например, работы “вскипятить воду” или “вскипятить молоко” могут быть разбиты при желании на более мелкие работы. Выбор множества работ для некоторого плана зависит от необходимого уровня анализа. Очень часто первое разбиение бывает грубым, при этом ориентируются на основные действия процесса. Дальнейшее разбиение направлено на выявление зависимостей внутри групп работ, соответствующих более низкому уровню деятельности.
2. Работа может соответствовать заданию, выполнение которого сопряжено с определёнными усилиями; наоборот, работа может быть бездеятельной, например, ожидание чего-то, что должно произойти (для рассмотренного примера это будет ожидание кипения воды).
3. Иногда в множество работ полезно включить фиктивную работу
. Это работы, которые не занимают времени и для которых не используются никакие ресурсы.
4. Имеется несколько специальных случаев, зависимостей между работами, которые должны быть рассмотрены при построении сетевых моделей (например, параллельное выполнение работ, зависимость одной работы от нескольких предшествующих и т.п.).
Событие
. Очевидно, что если какая-либо работа может быть начата только после окончания нескольких определённых работ, то необходимым и достаточным исходным условием для её начала являются лишь сумма частных результатов этих работ, то есть их суммарный результат. Этот суммарный результат и принято называть термином событие. Событиеозначает точку во времени, которая отделяет различные стадии осуществления проекта.
Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним – начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ. Среди событий сетевой модели выделяют начальное и конечное события. Начальное событие не имеет предшествующих работ и событий, относящихся к рассматриваемому в модели комплексу работ. Конечное событие не имеет последующих работ и событий.
Пример 9.3
В задании “вскипятить чайник воды” (пример 9.1) мы можем выделить три точки времени, которые называются событиями:
* - время начала выполнения задания (начальное событие);
* - время, когда мы ставим чайник на конфорку после завершения работы “наполнить чайник”;
* - время начала кипения, характеризующее конец выполнения задания (конечное событие).
Графическое представление расписаний работ
Существует два основных вида графического представления расписаний (графиков) работ. Это сетевые графики и диаграммы Ганта. Мы вначале рассмотрим графическое представление в виде классических сетевых графиков (опираясь на упоминавшуюся выше теорию графов), а в конце главы продемонстрируем представление возможные модификации сетевых графиков, а также представление расписаний в виде диаграмм Ганта.
Графическое изображение событий и работ
. В сетевых графиках работы обычно изображаются стрелками (т.е. направленными дугами) графа. Действительные работы изображаются на сетевом графике сплошными стрелками, а фиктивные работы - пунктирами. Описания работ при желании могут записываться вдоль стрелок. События должны быть занумерованы. Как правило, вершины графа обозначаются некоторыми геометрическими фигурами (например, кружочками). Внутри этих фигур проставляется соответствующий номер. Описание события может быть тоже записано внутри кружочка.
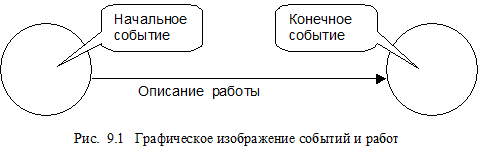

Работа должна быть выполнена в течение времени между двумя событиями, обозначенными своими номерами в концах соответствующей стрелки. Событие, соответствующее началу стрелки, называется начальным (или предшествующим) событием; конец стрелки называют конечным (или последующим) событием. Любая работа может быть определена своими числами, которые соответствуют начальным и конечным событиям.
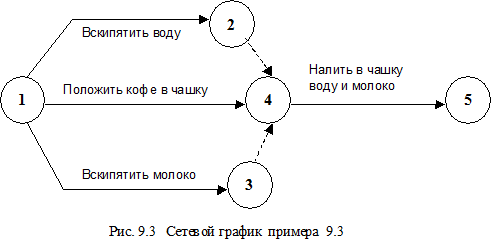
На рис. 9.1 - 9.3 иллюстрируются графические изображения сетей.
Замечания
1. Фиктивные работы (время выполнения равно нулю) необходимы для изображения параллельных работ. Три параллельные работы – “вскипятить воду”, “вскипятить молоко”, “положить в чашку кофе” - имеют одни и те же начальные и конечные события; для большей ясности события 2 и 3 (которые соответствуют событию 4) показаны на графике. Фиктивные работы 2 - 4 и 3 - 4 обозначены пунктиром.